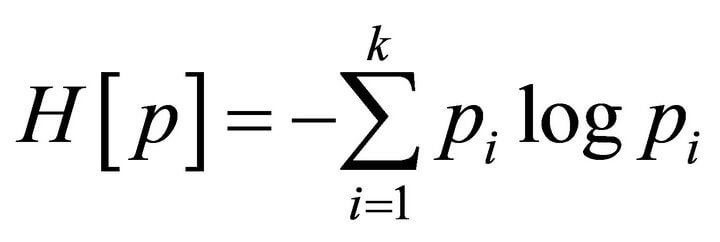“信息量” 到底有多大？

前言

生活中，我们常说 “啊，这个信息量很大呀！”。但所谓信息量大，到底有多大？可以量化吗？根据香农的理论，答案是肯定的。

信息量的度量

信息量实际上是事件不确定度的度量，越不确定的事件，对其的描述就包含越多信息。 举例来说，“明天太阳东边升起”，这句话是没有任何信息量的，因为我们都知道太阳总是东升西落。

香农为我们总结了信息量的计算方法：一条消息的信息量等于log(1/P)，其中底数大于1，通常为2，P为消息描述的事情发生的概率。根据这个公式，P越小信息量越大、P越大信息量越小。举例来说：“这次他买彩票中了头奖”，这个信息量非常大；“这次他买彩票没中奖”，这个信息量就很小。

当然，事情并非绝对。“太阳东升西落”作为一条自然知识，在一些情况下还是具有信息量的：假设一个人完全不知道太阳从哪边升起，即可能1/2为东升西落，1/2为西升东落，此时“太阳东边升起西边落下”这个描述对他而言还是有信息量的：信息量按2为底为log2=1bit。（显然，等他明白后，再告诉他太阳从哪边升起来，就又变得没信息量了:D）。

从中彩这个例子看，描述同一件事情的消息，其信息量既可能很大，也可能很小。我们要筛选更有价值的消息，就有必要知道消息的平均信息量，即信息量期望。因此我们引入信息熵。

信息熵

描述消息的平均信息量，即信息量的期望，计算公式如下图图：

还是举例来说：我在老家钓鱼。 “这次钓上来的是xx”，这句话的期望信息量对我而言其实不高，因为我早已知道老家鱼塘里钓到罗非鱼的概率比其他鱼、螃蟹的概率要大得多。假设钓到罗非鱼的概率为1/2，钓到其他鱼的概率为1/4，钓到虾的概率为1/8，钓到青蟹的概率为1/8。那么“这次钓上来的是x”的信息熵为1/2*1+1/4*2+1/8*3+1/8*3=7/4bit